Extracting the Private Key from a TREZOR

There were some dis­cus­sions on red­dit wheth­er TREZOR, a hard­ware wal­let for se­curely stor­ing Bit­coins, can be at­tacked us­ing side chan­nels like power fluc­tu­ations, elec­tro­mag­net­ic ra­di­ations or sim­il­ar. Such an at­tack would al­low for re­triev­ing the private key that gives ac­cess to the Bit­coins stored on the TREZOR. Usu­ally the dis­cus­sions of side-chan­nel at­tacks men­tion the code that signs a Bit­coin trans­ac­tion. To sign a trans­ac­tion on the TREZOR, you need to enter the secret PIN first. So this is not use­ful in the scen­ario where the ad­ver­sary has phys­ic­al ac­cess to the device but does not know the PIN.

However, also the gen­er­a­tion of the pub­lic key may leak some in­form­a­tion via a side chan­nel. Un­til firm­ware 1.3.2 of TREZOR this was not PIN pro­tec­ted. There­fore, I in­vest­ig­ated wheth­er it is pos­sible to use a side chan­nel to re­cov­er the private key from the pub­lic key com­pu­ta­tion.

I in­formed Satoshi Labs of my res­ult first, and this is why the latest firm­ware 1.3.3 will ask for a PIN when com­put­ing the pub­lic key. Also they in­cluded my sug­ges­ted patches in this firm­ware that will re­duce the in­form­a­tion leaked through side-chan­nels dur­ing com­pu­ta­tion of pub­lic keys, sig­na­tures, and de­cryp­tion.

This page ex­plains, how you can re­cov­er a private key from a TREZOR, if it still runs with firm­ware 1.3.1. It leaves out some cru­cial steps in or­der to make it not too simple for any­one read­ing this page. Non­ethe­less, this will hope­fully give you an in­cent­ive to up­date your TREZOR soon. Also, if you have pass­phrase pro­tec­tion, this at­tack does not work even with firm­ware 1.3.1, so you may con­sider adding that, too.

The Setup

I found a cheap os­cil­lo­scope (Hantek 6022BE) for 62 EUR. (By now, the price has ris­en to 73 EUR at Amazon). The goal was to meas­ure power con­sump­tion of my TREZOR over time to see wheth­er I can de­tect which code it is ex­ecut­ing or even re­cov­er the private keys.

To meas­ure the power con­sump­tion, I meas­ured the cur­rent go­ing through the USB cable. Since an os­cil­lo­scope can only meas­ure voltage, I in­ser­ted a 10 Ohm res­ist­or (for 0.05 EUR) in­to the mass wire of the USB cable. Thus, the voltage over this res­ist­or is dir­ectly pro­por­tion­al to the cur­rent through the res­ist­or, which is more or less pro­por­tion­al to the power con­sump­tion of the TREZOR.

A First Re­sult

The above graph­ic shows the power con­sump­tion of a TREZOR over time on start-up. The ho­ri­zont­al ax­is is the time in seconds, the ver­tic­al ax­is the voltage over the res­ist­or. The TREZOR was con­nec­ted while the web­site mytrezor.com was open in the back­ground. When the TREZOR is de­tec­ted the PC will ask the TREZOR for the pub­lic key. If the TREZOR is not pass­phrase pro­tec­ted, it wakes up, com­putes the mas­ter private key from the seed and then the pub­lic key from the private key.

In the fig­ure above, dif­fer­ent phases can be dis­tin­guished. The reg­u­lar spikes (click on the im­age for a lar­ger ver­sion) are caused by the dis­play, which runs at about 90 Hz. The power con­sump­tion of the dis­play de­pends on the num­ber of white pixels in the cur­rent line. Thus it is highest in the area where the pro­gress bar is dis­played. In the middle of the graph where the mas­ter private key is com­puted, you can see the spikes get­ting high­er be­cause the pro­gress bar gets filled. It is also ob­vi­ous where the dis­play is swiped to the left and cleared in the pro­cess. The power con­sump­tion goes slowly down at these places.

To com­pute the mas­ter private key, an al­gorithm called PBKDF-2 is ex­ecuted. Dur­ing this peri­od, the power con­sump­tion of the pro­cessor is high­er than when the al­gorithm pauses to re­fresh the dis­play (which it does eight times). After the last re­fresh the pub­lic key of the TREZOR is com­puted. When zoom­ing close in­to the dif­fer­ent parts, one can dis­tin­guish the PBKDF-2 al­gorithm from the part where the pub­lic key is com­puted.

Here we zoomed in­to the PBKDF-2 part of curve. This is from the first part of pb­k­df, where the pro­gress­bar is not yet filled. In the middle you can see a part of lower power con­sump­tion where the func­tion ole­dRe­fresh is called. Also you can see clearly see the reg­u­lar cycle caused by the 90 Hz re­fresh rate of the dis­play. Each cycle con­tains two spikes, which are caused by the lines above and be­low the pro­gress­bar. There are sev­er­al small spikes, which are caused by the SHA-512 op­er­a­tions that the PBKDF-2 al­gorithm per­forms. The fol­low­ing graph­ic shows them in more de­tail.

This fig­ure dis­plays a single dis­play re­fresh cycle, which takes about 11 milli seconds. In this graph­ic the in­di­vidu­al sha-512 cycles are clearly vis­ible ex­cept at the part where the power con­sump­tion of the dis­play (caused by dis­play­ing the pro­gress­bar) muffles the sig­nal of the pro­cessor.

Al­though the single cycles are clearly vis­ible, they look very sim­il­ar. The small dis­tor­tions are prob­ably caused by the dis­play. It is nearly im­possible to get any in­form­a­tion about the ac­tu­al val­ues used in the SHA-512 com­pu­ta­tion. The vari­ations in the power con­sump­tion are mainly caused by dif­fer­ent in­struc­tions, dif­fer­ent cache misses or branch mis­pre­dic­tions, in­stead of the dif­fer­ent bits in the in­put data.

Ana­lys­ing the Key De­riv­a­tion Func­tion

I was more in­ter­ested in de­term­in­ing the private key. In this sec­tion I will there­fore look in­to the key gen­er­a­tion. To avoid noise from the dis­play, I set a blank home screen. You can con­sider this as cheat­ing as chan­ging the home screen re­quires the PIN. However, an un­scru­pu­lous ad­ver­sary may just break open the case and rip off the dis­play to achieve the same ef­fect. The fol­low­ing graph­ic shows the com­pu­ta­tion of the mas­ter pub­lic key m/44'/0'/0'/0.

In the above graph­ics, there are four spikes, which mark the start of the bip32 de­riv­a­tion steps. If you care­fully count the small spikes in between, you can de­term­ine the num­ber of point_adds used to com­pute each pub­lic key. To get a feel­ing what goes on in this part, I put the pseudo code of the key de­riv­a­tion func­tions here.

hdnode_private_ckd_cached(HDNode *inout, int *i, int count) {
   ... some code looking up the key in the cache ..
   for (j = 0; j < count; j++)
      hdnode_private_ckd(inout, i[j])
}

hdnode_private_ckd(HDNode *inout, int i) {
   ... data = private/public key + i ...
   I = hmac_sha512(inout->chaincode, data)
   inout->chaincode = I[32:]
   inout->private_key += I[0:32];
   inout->public_key = scalar_multiply(inout->private_key)
}

// compute point private_key * G.
scalar_multiply(bignum256 *private_key) {
   iszero = 1
   for (int i = 0; i < 255; i++) {
      if (privatekey & (1 << i)) {
         // do two bits at a time.
         twobits = (privatekey >> i) & 3;
         // lookup twobits * 2 ^ i * G in a big table.
         toadd = bigtable[twobits][i];
         if (iszero) {
	    res = toadd;
            iszero = 0;
         } else {
            res = point_add(res, toadd);
         }
         i++; // skip another bit
      }
   }
   return res;
}

point_add(point *a, point *b) {
   ... some conditons that are usually false ...
   bn_inverse(b->x - a->x);
   ... some multiplications ...
}

bn_inverse(bignum256 *a) {
   ... some talkative function leaking
   a lot of random information about the 
   input a over my side-channel ...
}
  

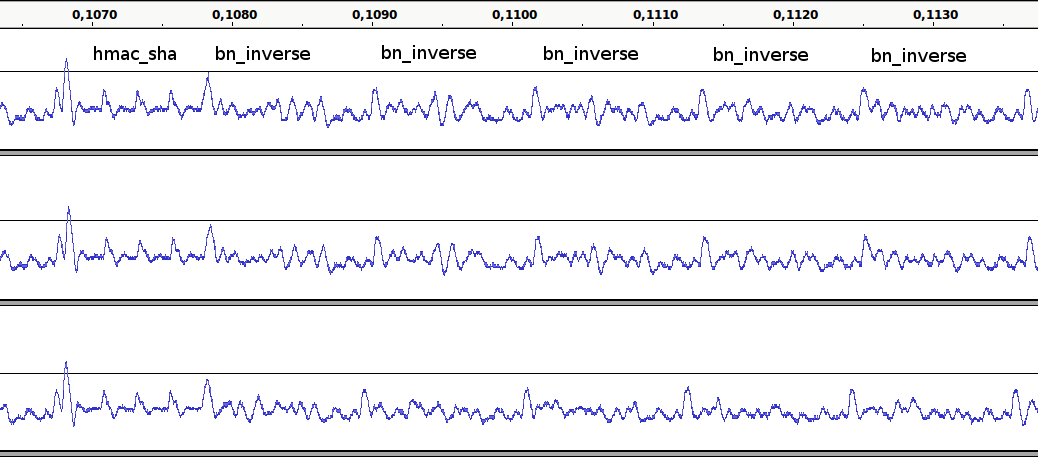
The fol­low­ing graph­ic shows the first part of a key de­riv­a­tion step in more de­tail and com­pares dif­fer­ent runs of the al­gorithm.

The first and second row show the com­pu­ta­tion of a pub­lic key for the same private key in two dif­fer­ent runs. The third row shows a com­pu­ta­tion of a pub­lic key for a dif­fer­ent private key. You can clearly see the SHA-512 cycles at the be­gin­ning that we already have seen in the zoomed in part of the PBKDF-2 al­gorithm. These are needed by the BIP32 al­gorithm to com­pute the child private key. After these cycles, the com­pu­ta­tion of the pub­lic key be­gins. To com­pute the pub­lic key, the func­tion scalar_multiply calls the func­tion point_add for each one bit oc­cur­ring in the private key. You can see the start of this part by a small spike. Most time of the point ad­di­tion is taken by the func­tion bn_inverse. This is a par­tic­u­larly in­ter­est­ing func­tion, since the code it is ex­ecut­ing is de­pend­ent on the in­put and it looks dif­fer­ent for every in­put, with which it is called. You can see that it pro­duces are ran­dom look­ing pat­tern. In the end there are a few mul­ti­plic­a­tions, that will again form two reg­u­lar small spikes fol­lowed by a big spike, where the next point ad­di­tion starts.

If you com­pare the three rows, you can see that the pat­tern caused by the func­tion bn_inverse looks very dif­fer­ent each round, but is the same if it is called on the same in­put, as it is done in the first and second row.

How to Re­cov­er the Pri­vate Key

One can clearly see the one bits in the private key, as these cause the point ad­di­tion to be called, which is clearly vis­ible. I hoped that one could see the zero bits in the private key that are skipped by scal­ar_mul­tiply. However, the time these op­er­a­tions take is too short to be vis­ible. So the dir­ect ap­proach to read the bits from the wave does not work.

However, the in­put de­pend­ent fin­ger­print of the bn_inverse func­tion is enough to re­cov­er the private key. The idea is that the in­put of the first bn_inverse func­tion de­pends only on the first two points ad­ded in the scalar_multiply loop. At this time the func­tion will have pro­cessed only a few of the low­est bits of the private key. One can gen­er­ate all the pos­sible val­ues for the low­est bits of the key, com­pute the cor­res­pond­ing pub­lic keys on a ref­er­ence TREZOR, and re­cord the fin­ger­prints of bn_inverse. These can be com­pared with the fin­ger­prints of the vic­tim TREZOR. On av­er­age one has to check 26.5 fin­ger­prints un­til one finds a match­ing fin­ger­print and thus the low­est bits. The later steps get even easi­er; for them only 5.5 fin­ger­prints have to be checked on av­er­age.

I have re­covered 128 bits of a private key as a proof of concept. It took me about two hours and it would take the same time to re­cov­er the second half. The main prob­lem is that one needs a ref­er­ence TREZOR and use it to re­trieve the ne­ces­sary fin­ger­prints of the bn_inverse func­tions. This work has to be re­peated for every private key.

There is no need to have ex­ten­ded ac­cess to the TREZOR you want to break. A simple re­cord­ing of one key de­riv­a­tion (which can be done in a few seconds) give you all the in­form­a­tion you need from this TREZOR. The ex­act fin­ger­print de­pends on the ex­act firm­ware, though. I guess that the align­ment of the func­tion is im­port­ant, i.e., wheth­er it crosses a cache line. However, the fin­ger­print is close enough to re­cog­nise it, even if the firm­ware is dif­fer­ent.

Im­prove­ments to Firm­ware

In re­ac­tion to these res­ults, PIN pro­tec­tion was ad­ded for com­put­ing pub­lic keys. This should pre­vent most side-chan­nel at­tacks.

Fur­ther­more, I sug­ges­ted a few im­prove­ments to the firm­ware that should rem­edy this prob­lem. The first im­prove­ment was only planned to give a slightly bet­ter per­form­ance to the bn_inverse func­tion; not even re­mov­ing the in­put de­pend­ent tim­ing. Non­ethe­less, it made the func­tion com­pletely in­vis­ible for my os­cil­lo­scope. Why did this hap­pen? My best guess is that be­cause I re­moved some du­plic­ated code, the same code path is used throughout the in­ner loop, while the pre­vi­ous code switched between the u is even and v is even code paths, de­pend­ing on the in­put.

However, the ex­act tim­ing of the func­tion still de­pends on the in­put. There­fore, it may still be pos­sible to re­cov­er the private key by ob­serving the dur­a­tion of each point_add.

This seg­ment starts when the get_public_node pack­age has just been re­ceived. At the be­gin­ning there is again the HMAC-SHA256 com­pu­ta­tion. As you can see the calls to bn_inverse pro­duce an al­most flat sig­nal. The peaks are caused by the fi­nal mul­ti­plic­a­tions in point_add.

The second patch set gives al­most con­stant time to the scalar_multiply func­tion. The only in­put de­pend­ent tim­ing is in a fi­nal bn_inverse call that is ran­dom­ised and is only called at the very end, when the full key has been pro­cessed. This should make it im­possible to re­cov­er any in­form­a­tion about the private key. An­oth­er side-ef­fect of this patch is that the sig­nal is even more si­lent.

This seg­ment starts near the end of a scalar_multiply call. You can see four calls of point_jacobian_add fol­lowed by bn_inverse called from jacobian_to_point. Then the next pub­lic key is de­rived and there is again an ap­plic­a­tion of HMAC-SHA256. After a point_to_jacobian there fol­lows the reg­u­lar se­quence of point_jacobian_add.

There is still a table look-up for the point in scalar_multiply and I'm not sure if this makes prob­lems. In prin­ciple by de­tect­ing cache misses one could get some in­form­a­tion about the private keys. However, I could not de­tect a dif­fer­ence between cache hit or miss with my hard­ware.

Al­though the code is not per­fect, it should make side-chan­nel at­tacks much more dif­fi­cult. With my tech­nique (check­ing the power con­sump­tion at the USB cable), I can­not see any way to re­cov­er the private key from a side chan­nel at­tack on scalar_multiply. Also ana­lys­ing elec­tro­mag­net­ic ra­di­ation or acous­tics shouldn't be feas­ible, as they have even less in­form­a­tion. It may be pos­sible to re­cov­er more in­form­a­tion by open­ing the device and meas­ur­ing the power con­sump­tion dir­ectly at the pro­cessor. This re­quires phys­ic­al ac­cess and in that case you now need the PIN for every op­er­a­tion.

Down­loads

Time-line

• 2015-03-21: firm­ware 1.3.2 was tagged.
• 2015-03-24: firm­ware 1.3.2 bin­ary ad­ded to web­wal­let-data re­pos­it­ory, but not yet pub­lished.
• 2015-03-24: my os­cil­lo­scope ar­rived. In an­ti­cip­a­tion I had everything pre­pared.
• 2015-03-26: first res­ults. I in­formed stick and slush at that time. They asked to delay pub­lic­a­tion un­til they can re­solve the is­sues in a new firm­ware re­lease 1.3.3.
• 2015-03-29: I man­aged to ex­tract a big part of a private key by ap­ply­ing the tech­nique sketched above.
• 2015-03-30: PIN pro­tec­tion ad­ded to firm­ware code. My patches to the rel­ev­ant cryp­to­graph­ic func­tions were merged in­to the TREZOR re­pos­it­ory.
• 2015-04-07: firm­ware 1.3.3 re­leased.
• 2015-04-09: this page was pub­lished.

Con­clu­sion

Side chan­nel at­tacks are not as dif­fi­cult as many people think. A simple power ana­lys­is re­quires only a simple os­cil­lo­scope and that can hardly be called ex­pens­ive labor­at­ory equip­ment. You also need ba­sic sol­der­ing skills and deep know­ledge about the code that is run­ning. It took only a single re­cord­ing of the com­pu­ta­tion of the pub­lic key, to re­cov­er the private key. On the bright side, this simple side chan­nel at­tack can be mit­ig­ated by us­ing con­stant-time code and as I showed this code does not have to be slow.

The new firm­ware 1.3.3 is im­mune against this at­tack since it (1) re­quires a PIN to com­pute the pub­lic key and (2) uses branch-free com­pu­ta­tions for de­riv­ing the pub­lic key from the private key.

There is no com­plete pro­tec­tion against all kind of at­tacks. If your TREZOR gets stolen and it has no pass­phrase pro­tec­tion (or if the pass­phrase is weak), you should trans­fer the coins to a dif­fer­ent wal­let. There are oth­er at­tack vec­tors like fault in­jec­tion that could still be used and may get around the PIN pro­tec­tion. Ba­sic­ally, they use the fact that the mi­cro­pro­cessor does un­ex­pec­ted things if power sup­ply or the clock sig­nal is broken. These are much more dif­fi­cult to per­form, but they are prob­ably less ex­pens­ive than us­ing an elec­tron mi­cro­scope to read the seed from the chip. Also, there may be a bug in the mi­cro­pro­cessor that al­lows for cir­cum­vent­ing the read-out pro­tec­tion.

Dis­claim­er

I am not in­volved with Satoshi Labs or any of their com­pet­it­ors. I own two TREZORs my­self (one for stor­ing my sav­ings and one for hacks like this) and I am still think­ing hard­ware wal­lets are the best way to pro­tect against most at­tack vec­tors. Prob­lems like this are to be ex­pec­ted in any new product and TREZOR is barely a year old now. It is more im­port­ant that these things get fixed in a timely man­ner.

If you want to sup­port my work, you can send bit­coins to 1D2XuL4uH52qgy2FerzNkeX1jJ9gCJwqgq